Superficie

En matemática, una superficie es una variedad bidimensional, es decir, un objeto topológico que, intuitivamente hablando, es localmente "parecido" al plano cartesiano <math>\mathbb{R}^2</math> (tecnicamente localmente homeomorfo al plano). Eso significa que para cada punto de una superficie hay una vecindad de P (una pequeña región que la rodea) que es homeomorfa a un disco abierto de <math>\mathbb{R}^2</math>. Esa propiedad homeomorfismo con el plano permite construir un sistema de coordenadas local bidimensional en torno a cualquier punto en la superficie. Se puede llamar al homeomorfismo local que va de la superficie a <math>\mathbb{R}^2</math> como carta y al inverso (de este homeomorfismo) parametrización. No siempre es posible parametrizar una superficie con un único homeomorfismo local.

En física, una superficie es una región "delgada" del espacio o interfase que separa dos fases de propiedades diferentes. De hecho una propiedad importante de las superficies físicas es que algunas propiedades físicas importantes tienen una discontinuidad importante. Algunos artículos que tratan con las superficies desde el punto de vista de la física son: tensión superficial, interfase química, rugosidad, etc.

Para clasificación, ver artículos independientes: Variedad diferenciable, algebraica y topológica

Superficies en matemática

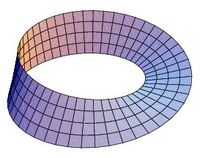
También las superficies se distinguen según sean orientables o no. Se dice que una superficie es no orientable si contiene al menos una sub-superficie que es homeomorfa a una banda de Möbius cerrada. Caso contrario se dice orientable.

Superficies cerradas

Una superficie cerrada es una superficie que divide el espacio en dos regiones diferentes y disjuntas: una interior a dicha superficie que sea de volumen finito y una exterior a dicha superficie. En otras palabras, una superficie cerrada es la superficie exterior de un objeto con volumen, como por ejemplo una esfera. Es posible entonces distinguir entre dentro de la esfera y fuera de la esfera. Este término se utiliza para diferenciarlas de las superficies que no encierran nada en su interior, como un plano infinito.

La esfera, el toro, el plano proyectivo, la botella de Klein son ejemplos de superficies cerradas, es decir, superficies sin frontera.

Un disco (en <math>\mathbb{R}^2</math>), un cilindro y la banda de Möbius son ejemplos de superficies con frontera. Como la imagen de la derecha. Haciendo lo mismo que en el siguiente párrafo.

Clasificación de superficies

Un importantísimo resultado matemático es el teorema de clasificación de superficies cerradas, el cual afirma que toda superficie cerrada (es decir, sin frontera o borde) es homeomorfa a algún miembro de las siguientes tres familias de superficies:

1. la esfera;
2. la suma conexa de <math>g\,</math>-toros, siendo <math>g \geq 1</math>;
3. la suma conexa de k planos proyectivos reales, siendo <math>k \geq 1</math>.

Dicho de otra manera, las superficies anteriores son todas las superficies cerradas que existen (salvo homeomorfismo). La superficies de las dos primeras familias son orientables. Es conveniente combinar las dos primeras familias, considerando la esfera como la suma conexa de cero toros. El número g de toros involucrados en la construcción se denomina género de la superficie. Puesto que la esfera y el toro tienen características de Euler 2 y 0, respectivamente, se deduce que la característica de Euler de la suma conexa de g toros es precisamente <math>2-2g\,</math>.

Las superficies de la tercera familia son no-orientables. La característica de Euler del plano proyectivo real es 1, así la suma conexa de k de ellos es is <math>2-k\,</math>.

De todo esto se sigue, que una superficie cerrada está determinada -salvo homeomorfismo- por dos propiedades: el valor numérico de su característica de Euler (o su género) y si es o no-orientable.

Es posible clasificar también las superficies que no son cerradas (es decir, con frontera). Esto se obtiene como el esquema anterior, añadiendo el número de fronteras que tiene la superficie.

Enlaces externos

• Surface en la Enciclopedia en-línea de la Springer-Verlag

El contenido de esta página sobre matemática necesita ser ampliado y mejorado.
Haciéndolo ayudarás a mejorar la enciclopedia.
Puedes ayudarte con la Wikipedia.

:El contenido de este artículo incorpora material de una entrada de la Wikipedia, publicada en español bajo la licencia GFDL.